Рациональные формы сечения деталей, работающих на изгиб

Детали, работающие на изгиб (в основном, балки), весьма распространены в любых конструкциях, в том числе и в машинах. Особенно сильно изгибу подвер­гаются детали, у которых поперечные размеры значительно меньше продольных.

Изгибом называют вид деформации, характеризующийся искривлением оси деформируемого объекта (балки, плиты, оболочки и т. д.) под действи­ем изгибающих моментов.

Снижение напряжений в деталях, подверженных деформации изгиба, может быть достигнуто за счет уменьшения величины расчетного изгибаю­щего момента и увеличения момента сопротивления внутренних сил. Раци­ональным размещением опор можно добиться уменьшения расчетного из­гибающего момента, а выбором рациональной формы сечения детали — увеличения момента сопротивления.

Предположим, вы захотели сломать палку. Ухватившись руками за ее края, вы прикладываете палку серединой к колену и, сгибая, ломаете ее. Причем чем длиннее палка, тем легче ее сломать, чем короче — тем труднее. Последовательно уменьшая длину палки, вы заметите, что на каком-то этапе оставшийся кусок палки не будет поддаваться изгибающему моменту. Это объясняется тем, что при последовательном сближении рук (точек приложе­ния сил) длина плеч уменьшается, и изгибающий момент, равный произведе­нию силы на плечо, также уменьшается. Когда его величина станет меньше момента сил сопротивления, палку этим способом сломать невозможно.

Отсюда можно сделать вывод, что для деталей, работающих на изгиб, следует подобрать такое соотношение величины поперечного сечения дета­ли к расстоянию между точками опоры, при котором детали наименее под­давались бы деформации изгиба.

На рис. 73 показан пример двухопорной установки зубчатого колеса. Ес­ли расстояние между опорами сократить в 3 раза, то максимальный изгиба­ющий момент и напряжения в вале уменьшатся также почти в 3 раза, а максимальный прогиб — в 27 раз.

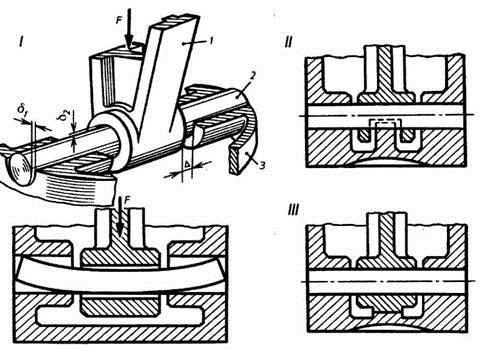
Во многих случаях жесткость системы удается увеличить введением дополнительных опор. На рис. 74 показаны приемы увеличения жесткости и прочности шатунно-поршневого сочленения. Часто применяемая конструкция (рис. 74, I), в которой палец 2 работает на изгиб, обладает малой жесткостью, особенно, если в сочленении имеются радиальные (?₁. ₂ ) и боковые (?) зазоры. Упрочнение шатунно-поршневого сочлене­ния достигают увеличением числа опор и уменьшением пролетов, под­вергающихся изгибу. В усовершенствованные конструкции (рис. 74, II и III) введены дополнительные опоры: в одном случае поршневой палец не­посредственно опирается на поршень 3, в другом — на головку шатуна 1. Ввиду сокращения вдвое плеча действия сил напряжение изгиба умень­шилось в 2 раза, а деформация — в 8 раз по сравнению с исходной конст­рукцией.

Рассмотрим теперь консольную балку. Возьмем доску, закрепленную одним концом в неподвижной опоре, и приложим к ее свободному концу силу F (рис. 75). Будут ли все сечения равно- опасны? Опыт говорит, что нет. Возможные разрушения могут произойти прежде всего в сечениях, совпадающих с заделкой. Дело в том, что момент, создаваемый силой F (изгиба­ющий момент), в этом сечении будет наиболь­шим. Ведь величина момента зависит не толь­ко от величины силы, но и от ее плеча, и имен­но для сечений, совпадающих с заделкой, пле­чо наибольшее.

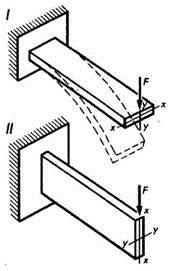
Нетрудно предвидеть, что в первом вариан­те (рис. 75, I) доска изогнется при сравнитель­но небольшой величине силы F. Во втором ва­рианте (рис. 75, II) для достижения того же ре­зультата понадобится значительно большая сила. Чем отличается положение балок? В первом случае деформируемые слои материала доски в сечении ближе расположены к нейт­ральной оси (x — х), а во втором (ось у — у) — дальше. Из предыдущего материала уже известно, что нейтральная ось (нулевая линия) — это геометрическое место точек поперечного сечения, в которых нормальные напряжения равны нулю.

Отсюда можно сделать вывод: поскольку основное сопротивление изгибу оказывают периферийные слои материала, целесообразно при изгибе при­менять брусья с сечениями, в которых материал расположен дальше от ней­тральной оси.

Этот пример помогает понять, почему рычаги машин, шатуны и другие детали, а также рельсы, балки, корпуса и рамы машин в плоскости дейст­вия изгибающего момента имеют особую форму сечения, при которой уси­лены части, наиболее удаленные от нейтральной оси. В целом эти сечения напоминают доску, поставленную на ребро (рис. 76).

При конструировании для увеличения жесткости изделия стремятся всемерно устранить изгиб, заменить его сжатием и растяжением.

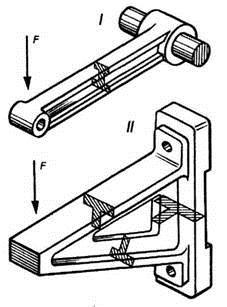
На рис. 77 показан пример конструктивного разгружения шатуна от из­гиба. Внецентровое приложение нагрузки F (рис. 77,I) вызывает в стержне шатуна дополнительные напряжения изгиба, из-за чего приходится увели­чивать сечение стержня, а следовательно, и массу конструкции. Тот же не­достаток, но в меньшей степени, присущ конструкции, приведенной на рис. 77, II. Здесь внецентровой изгиб возникает вследствие асимметрии сечения стержня относительно направления действия сил. Рациональной является конструкция с симметричными относительно нагрузки сечения (рис. 77, III). В этом случае нагрузка приводится к одному сжатию при прочих рав­ных условиях масса конструкции наименьшая.

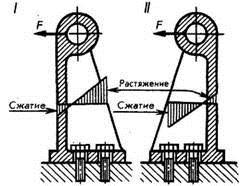
Пример нецелесообразного и целесообразного нагружения деталей на изгиб показан на рис. 78. В первом случае (рис. 78, I) кронштейн относи­тельно направления изгибающей нагрузки ориентирован нецелесообраз­но, так как ребро жесткости, способное воспринимать большие нагрузки сжатия, испытывает большие напряжения растяжения. Следует иметь в виду, что большинство хрупких конструкционных материалов, таких, как чугун, лучше сопротивляются сжатию, чем растяжению. В другом случае (рис. 78, II) соотношение между максимальными напряжениями сжатия ребра жесткости чугунного кронштейна и растяжения его стенки наиболее рационально.

Многие детали машин, подвергающиеся нагружению изгиба, имеют не­постоянное по длине поперечное сечение (кривошип, рычаги, шатуны, ва­лы и др.). Это объясняется различием моментов, действующих в разных участках детали. Рассмотрим это более подробно.

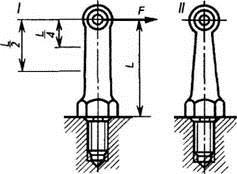
Предположим, что на стойку, ввернутую в плиту (рис. 79, I), действует сила F, которая стремится изогнуть стойку. Наибольший изгибающий мо­мент при этом равен произведению F • L: где L — высота стойки. Определим теперь изгибающий момент в некоторых сечениях стойки по высоте. На расстоянии L/4 от верхнего конца изгибающий момент равен (F • L)/4, по­средине стойки — (F • L)/2, у основания — F • L.

Но если в разных сечениях стойки действуют неодинаковые моменты, то размеры сечений стойки по высоте также следует выполнить неодинако­выми: в верхней части стойки поперечные сечения должны быть меньше, чем в нижней части (рис. 79, II). Если сравнить две конструкции стоек, то нетрудно заметить, что на вторую потребуется меньше материала, чем на первую.

Рациональными формами сечений деталей, работающих на изгиб, являют­ся двутавровые (рис. 80,I), швеллерные (рис. 80, II), коробчатые (рис. 80, III) и трубчатые (рис. 80, IV) полые сечения. Круглые полые сечения также эффективны при работе деталей на изгиб. Этим объясняется все более широкое применение этих сечений для вращающихся деталей, подвергающихся также изгибающим усилиям (например, для осей железнодорожных вагонов).

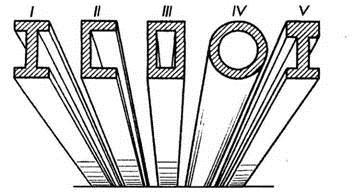
Если материал балки имеет различную прочность на растяжение и сжа­тие, то наиболее рациональным будет сечение в виде несимметричного дву­тавра (рис. 80, V).

Способность поперечного сечения сопротивляться деформации изгиба характеризуется осевым моментом сопротивления изгибу W. Величина W зависит от формы и размеров поперечного сечения и от его ориентации по отношению к изгибающей силе. К обозначению W добавляют индекс, соот­ветствующий обозначению нейтральной оси (например, W_х или W_y ), отно­сительно которой вычисляют момент сопротивления изгибу.

На рис. 81 приведена диаграмма соотношения моментов сопротивления W_x и W_y для некоторых профилей проката, широко применяющихся в ма­шиностроении.

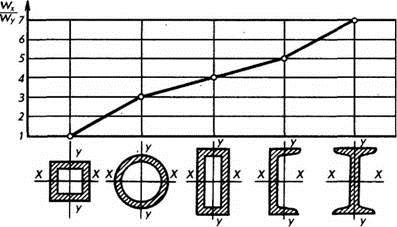
Из диаграммы видно, что отношение W_x /W_y колеблется в больших пре­делах от 1 до 7. В связи с этим для лучшего использования материала в де­талях с нагрузками в плоскостях «x—х» и «у—у» профиль проката следует выбирать в соответствии с величиной изгибающих моментов. Для стандарт­ных профилей типа двутавров и швеллеров величины осевых моментов со­противления изгибу приведены в справочниках.

Больше информации по теме: http://cherch.ru